0%

secure aggregation for federated learning

Posted on Edited on In Views: Valine:
Symbols count in article: 5.5k Reading time ≈ 9 mins.

Secure Aggregation for Federated Learning

引言

本工作由keith等(google)完成发表在2016年nips上。对于联邦学习，隐私性与安全性是首要的，为此可以接受模型性能的轻微下降。Secure Aggregation（以下简称SA)是一类从分布式群体\(u \in \mathcal{U}\)中获取统计量而不泄露单用户信息\(x_{u}\)的方法。在这篇文章中，作者提出了用于保护联邦学习中分布式梯度更新的单个用户梯度的协议，这项协议在效率以及稳定性上都做了考虑，在至多三分之一用户未完成协议时仍然能保证安全性。

SA4FL

在标准的联邦学习算法中，客户端使用本地数据对本地模型参数计算一次梯度更新\(\delta_{u}^{t}=\left|D_{u}\right| \nabla \mathcal{L}_{f}\left(D_{u}, \Theta^{t}\right)\)，这里\(D_{u}\)为客户端\(u\)所持有的训练数据，服务器则汇总来自客户端的梯度计算平均值\(\nabla \mathcal{L}_{f}(B, \Theta)=\frac{1}{|B|} \sum_{u \in \mathcal{U}^{\prime}} \delta_{u}^{t}\)，\(B=\bigcup_{u \in u^{\prime}} D_{u}\)为从客户端群体子群包含训练集的并，并使用这个平均值更新全局模型。

尽管客户端上传的参数相比数据包含有更强的隐私性，在一些工作中表明了我们仍然可以使用模型参数重构训练样例，使用SA协议可以保证我们至多能够从全局模型中重构数据，而无法知道数据与客户端的对应关系。

Protocol 0: 单轮掩码保护

假定所有的客户端都完成协议，并且拥有充足带宽的成对安全交换通道，该协议分为如下几步：

  1. 用户\(u\)对其余用户\(v\)生成\(k\)维整数均匀分布随机向量\(s_{u,v}\)，用户\(u,v\)在安全信道交换各自的\(s_{u,v}\)，并计算扰动\(p_{u,v}=s_{u,v}-s_{v,u}\). 注意有\(p_{u, v}=-p_{v, u}\)并规定\(u,v\)相等时\(p_{u,v}=0\);
  2. 用户\(u\)计算\(y_u=x_u+\Sigma_{v\in \mathcal{U}}p_{u,v}\)，并上传至服务器;
  3. 服务器汇总所有上传，计算\(\bar{x}=\Sigma_{u\in \mathcal{U}}y_u\)，正确性由以下等式保证：

\[ \bar{x}=\Sigma_{u\in \mathcal{U}}x_u+\Sigma_{u\in \mathcal{U}}\Sigma_{v\in \mathcal{U}}p_{u,v}=\Sigma_{u\in \mathcal{U}}x_u+\Sigma_{u\in \mathcal{U}}\Sigma_{v\in \mathcal{U}}s_{u,v}-\Sigma_{u\in \mathcal{U}}\Sigma_{v\in \mathcal{U}}s_{v,u}=\Sigma_{u\in \mathcal{U}}x_u. \]

以上为protocol 0的内容，它保证了用户\(u\)所拥有\(x_u\)的完全隐私性，因为用户实际上传的\(y_u\)包含了一项通过均匀采样产生的噪声，更重要地保证了服务器能够准确还原统计量\(\bar{x}\). 实际上，即便服务器通过某些方式访问到部分\(u\)的\(x_u\)值，这项协议仍然能保证剩余用户的信息安全性。

Protocol 1: 使用密信共享在含违协议用户情况还原统计量

protocol 0的问题在于，如果含有未将\(y_u\)上传至客户端的用户，那么服务器将无法还原所需统计量。

为了保证协议的稳定性，我们首先增加一个初始轮次，每个用户\(u\)都会生成一个公私钥对，并通过配对通道广播公钥给其余用户。之后所有由\(u\)传至\(v\)的信息都由服务器中转，但是首先会用\(v\)的公钥加密，形成一条安全认证信道。这使得服务器始终能观察哪些用户成功完成协议的各个轮次。

在选定\(s_{u,v}\)后增加密信共享轮次，每个用户使用\((t,n)-threshold\ scheme\)对每个\(p_{u,v}\)都计算\(n\)个share，\(n\)为用户总数。简单说明一下\((t,n)-threshold\ scheme\)的功能是将一个信息分成\(n\)份，使用其中不少于\(t\)份都可以还原信息，规定\(t>\frac{n}{2}\).

协议流程如下：

  1. 用户\(u\)生成公私钥对，通过用户间配对通道向其余用户广播公钥;
  2. 用户\(u\)对其余用户\(v\)生成\(k\)维整数均匀分布随机向量\(s_{u,v}\)，用户\(u,v\)在安全信道交换各自的\(s_{u,v}\)，并计算扰动\(p_{u,v}=s_{u,v}-s_{v,u}\);
  3. 用户\(u\)对拥有的每个secret，即\(p_{u,v}(\)\(v\in \mathcal{U}\))都计算其\(n\)个share，按照顺序依次用公钥加密后由服务器分发给其余用户\(v\)（每个\(v\)拿到的share都不同）。服务器记录参与secret share的用户群体，形成\(\mathcal{U}\)的子集\(\mathcal{U}_1\)，要求\(|\mathcal{U}_1|\ge t\). 由于每个\(\mathcal{U}_1\)中的用户都收到了本集合中其它用户的share，故而知道\(\mathcal{U}_1\)所代表用户名单;
  4. 用户\(u\)计算\(y_u=x_u+\Sigma_{v\in \mathcal{U}_1}p_{u,v}\)，并上传至服务器，服务器记录进行本次上传操作的用户，形成\(\mathcal{U}_1\)的子集\(\mathcal{U}_2\)（同样要求\(|\mathcal{U}_2|\ge t\)）;
  5. 服务器要求\(\mathcal{U}_2\)的每个用户\(u\)提供由\(\mathcal{U}_1\setminus \mathcal{U}_2\)发送的share，若\(\mathcal{U}_1,\mathcal{U}_2\)相同那么无需进行，考虑不同的情况（即有一部分用户没有上传\(y_u\)），由于\(|\mathcal{U}_2|\ge t\)，所以服务器能够还原这些secret: \(\{p_{u,v}|u\in \mathcal{U}_1\setminus \mathcal{U}_2,v\in \mathcal{U}_2\}\)，计算\(\bar{x}=\Sigma_{u\in \mathcal{U}_2}y_u-\Sigma_{u\in\mathcal{U}_2\Sigma_{v\in \mathcal{U}_1\setminus \mathcal{U}_2}p_{u,v}}\)，正确性由以下等式保证：

\[ \bar{x} = (\Sigma_{u\in \mathcal{U}_2}x_u+\Sigma_{u\in \mathcal{U}_2}\Sigma_{v\in \mathcal{U}_1}p_{u,v})-\Sigma_{u\in \mathcal{U}_2}\Sigma_{\mathcal{U}_1\setminus \mathcal{U}_2}p_{u,v}=\Sigma_{u\in \mathcal{U}_2}x_u+\Sigma_{u\in \mathcal{U}_2}\Sigma_{v\in \mathcal{U}_2}p_{u,v}=\Sigma_{u\in \mathcal{U}_2}x_u \]

然而当服务器谎报\(\mathcal{U}_1\setminus \mathcal{U}_2\)时，单个用户的隐私就会被泄露，如服务器向\(\mathcal{U}_1\setminus \mathcal{U}_2\)减少特定用户\(u_k\)，通过对比正确的\(\bar{x}\)与增加\(u_k\)后计算的\(\bar{x}'\)就可以知道\(u_k\)向\(x_{u_k}\)添加的噪声，从而获取\(x_{u_k}\)的值。

Protocol 2: 针对恶意服务器的双掩码保护

增加一轮掩码，服务器如果谎报则无法还原正确结果，也得不到任何有效信息。

首先每个用户\(u\)在生成\(s_{u,v}\)时均匀采样一个额外的随机\(k\)维向量\(b_u\)，在secret share的阶段也将\(b_u\)的share用公钥加密后由服务器中转给其余用户。

在产生\(y_u\)时，用户同样将其作为掩码加入\(y_u=x_u+b_u+\Sigma_{v\in \mathcal{U}_1}p_{u,v}\)，在去掩码阶段服务器必须明确选择让\(\mathcal{U}_2\)的用户提供\(\mathcal{U}_1\)发送的\(s_{u,v}\)或\(b_u\)的share其中之一，不能同时提供两者。

以单个\(\mathcal{U}_2\)中的用户\(u\)来说，对于\(u\)拥有的来自\(\mathcal{U}_1\setminus \mathcal{U}_2\)的share对（\(s_{u,v}\)及\(b_u\)的share），服务器应该要求\(u\)提供\(s_{u,v}\)的share，剩余来自\(\mathcal{U}_2\)则应要求提供\(b_u\)的share.

由于\(|\mathcal{U}_2|\ge t\)，故而sever能够还原\(\{b_u,u\in \mathcal{U}_2\}\)，以如下方式计算最终统计量： \[ \bar{x} = \Sigma_{u\in \mathcal{U}_2}y_u-\Sigma_{u\in \mathcal{U}_2}b_u- \Sigma_{u\in \mathcal{U}_2}\Sigma_{\mathcal{U}_1\setminus \mathcal{U}_2}p_{u,v} \] 若以其它方式选择share，如向\(\mathcal{U}_1\setminus \mathcal{U}_2\)增加用户，多获得一些\(p_{u,v}\)的信息的同时会损失\(b_u\)的信息，在结果上无法从别的选择方式中获得额外信息，并且不能正确还原统计量。

Protocol 3: 高效交换密信

协议2虽然在正确选择\(t\)后可以保证稳定和安全，但需要\(\mathcal{O}(kn^2)\)的交流次数。

注意到使用单个数值与安全伪随机生成器就可以生成伪随机向量，用户可以只交换标量值\(s_{u,v},b_u\)然后作为种子扩张成\(k\)维向量。

这里使用钥协定来更有效率地建立这些secret，每个用户生成一个Diffie-Hellman密钥\(s^{SK}\)与公钥\(s^{PK}\)，然后将公钥上传至服务器，服务器将所有公钥广播给所有用户，并保留备份。

用户\(u,v\)通过如下方式确定各自\(s_{u,v}\): \[ s_{u,v}=s_{v,u}=AGREE(S_u^{SK},S_v^{PK})=AGREE(S_v^{SK},S_u^{PK}) \] 这里\(AGREE(\cdot)\)为密钥协定算法。

然后以如下方式计算扰动，假定\(\mathcal{U}\)拥有全排序： \[ \begin{aligned}p_{u,v}&=PRG(s_{u,v}),u<v\\p_{u,v}&=0,u=v\\p_{u,v}&=-PRG(s_{u,v}),u>v \end{aligned} \] 服务器只需要知道\(s_u^{SK}\)就可以重构出\(u\)的所有扰动，因此u在secret share阶段只需要分发\(s_u^{SK},b_u\)的share即可。

protocol 3的安全性可以被证明与protocol 2一致

Protocol 4: 实践最小信任

SA4FLP4

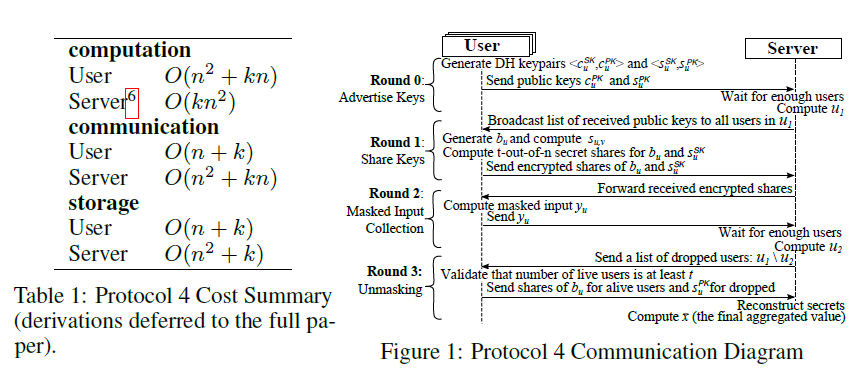
在上面的协议中，我们都假设用户间有安全的配对信道，需要给出更多细节。这里提出使用服务器中转密钥协议代替protocol 1描述的公私钥交换。

每个用户都会生成一个Diffie-Hellman密钥\(c^{SK}\)以及公钥\(c^{PK}\)，并将后者与\(s^{PK}\)一起公布。

这里指出服务器有可能进行中间者攻击，但出于几个理由这是可以容忍的：

  • 对于缺少认证机制的用户和预先存在的公钥架构这是不可避免的。只依赖联络阶段的非恶意性同样构成了信任最小：这一阶段的代码实现较短并且可以被空开编辑，向可信任第三方开源，或者通过一个能提供远程认证的可信计算平台来实现。
  • 这项协议在其余层面提高了安全性（除了服务器进行中间攻击外），并且提供了正向保密性（在密钥交换后的任何时候入侵服务器，攻击者都不会得到有用信息，即便所有数据和会话都被记录下来）

图片给出了protocol 4各项复杂度以及流程